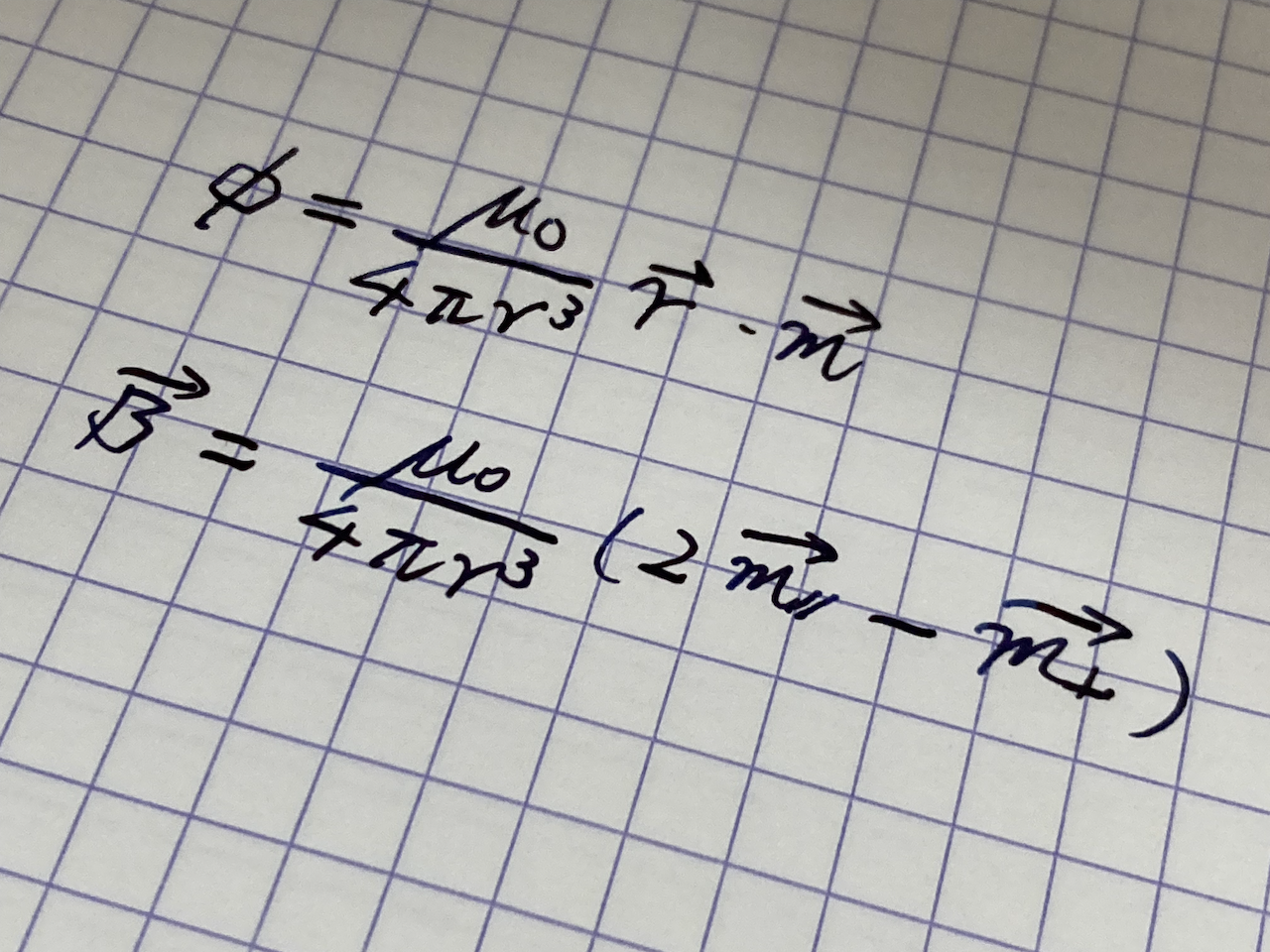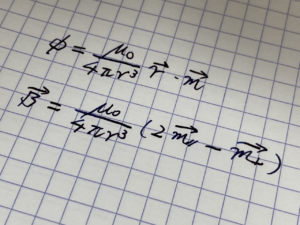この記事では、昨年2022年の国際物理オリンピック(International Physics Olympiad = IPhO)スイス大会の理論問題1の前半部分について解き方に踏み込んで紹介していきたいと思います。計算などの詳細は公式の解答例に記載してあるので、それを繰り返すことはしません。どういった考え方をすると解き方を思いつくのかというところに主眼を置きたいと思います。
なお、こちらの記事は物理オリンピックの出題範囲程度(≒理系の大学1年生程度)の物理の知識があることを前提にしています。前提知識なく問題の概要を知りたい方は前回の記事をご覧ください。

IPhO2022 理論問題1 磁石
それでは、IPhO2022 スイス大会の理論問題1の前半(Part A まで)について考え方を見ていきます。
実際の問題や解答例を確認したい方は、物理チャレンジのホームページ(日本語訳)か IPhO2022 のホームページ(英語原文)をご覧ください。以下の紹介では問題のネタバレを含みますので、自力で解きたい方はご注意ください。
全体について
理論問題1は電磁気学の分野から磁石についての出題です。ネオジム磁石を近づけたりくっつけたりした際に発生する力を計算することが問題の中心です。
まず、問題をざっと見渡すと以下の3つのパートに分かれています。
Part A: 磁石間の相互作用(4.5点)
Part B: 強磁性体との相互作用(3.5点)
Part C: (反)強磁性秩序(2.0点)
配点からは Part A の分量が重く、Part C の分量が軽くなっています。IPhO の問題では、(一般的な受験の問題とは異なり、)前のパートが解けない場合も後のパートが解けるような構成となっていることが多いです。もしも、Part A や Part B で躓いてしまった場合も、軽めのパートである Part C で点数を取っていくのは、実際のコンテストでは有力な選択肢です。
また、こちらの問題はかなり「ヨーロッパ的な」問題になっていると思います。
IPhO では開催国の委員会のメンバーが問題の原案を作成して、その原案を各国の役員が合議で検証・修正した後に、最終的な問題が決まります。そのため、問題の内容は開催国の特色が反映されたものになります。
アジアでの大会では、どのような手順で考えるべきかという詳細な部分まで誘導がついた問題が多い(そのため小問数も多くなる)という印象です。一方で、ヨーロッパの大会では、様々な解法が考えられる問題に対して、どのような手順で考えるかというところまでコンテスタントに自由に考えさせる問題が多いです。
そういった観点から見ると、この問題は解法の自由度が高い「ヨーロッパ的な」問題になっていると言えます。このような問題では、優れた解法を思いつくと短時間で解ける一方で、計算量の多い解法をとってしまうと時間をロスしてます。そのため、時間配分に気をつけながら解く必要があり、制限時間のある実際のコンテストでは扱いの難しい問題でしょう。
Part A: 磁石間の相互作用
このパートは前半と後半に分かれています。前半では100円玉程度のサイズ感の円盤形の磁石を扱い、後半では球形の磁石を扱います。
円盤形の磁石の間に働く力
小問A1
2つの円盤形磁石に間に働く力を計算します。配置としては、磁石間の距離は十分離れています。
磁石間の距離が十分離れていることを利用して近似を行い、計算を簡略化します。問題文のヒント(ヒント2)にもあるように、磁石間の距離が十分離れている場合は、磁石の作る場は磁気双極子の作る場と同じになります。従って、一方の磁石がもう一方の磁石の箇所に作る磁場がわかり、相互作用のエネルギーを磁場中の磁気双極子のエネルギーとして近似計算できることになります。エネルギーを距離で微分することで両者の間に働く力を求めることができます。
小問A2
円盤形磁石の作る磁場を遠方で再現するために、磁石の円周に流す必要がある電流の値を計算します。
電流の作る磁場の磁気モーメントが、電流と電流の囲む面積に等しいという知識があれば、磁気モーメントの値を比較する単純計算で、必要な電流の値を計算することができます。
一方、知識がない場合は、磁石が作る磁場と円電流が作る磁場とを遠方で比較して、それらが一致する電流を計算することになります。円電流の作る磁場を一般の場所で計算することは手間がかかるので、円盤の軸上で作る磁場を計算するのが良いでしょう。電流の作る磁場は Biot-Savart の法則で計算することができます。
小問A3
A1 と同様に2つの円盤形磁石に働く力を計算します。但し、今回は磁石間の距離が十分近いという違いがあります。
磁石間に働く力を円盤上に分布した磁気モーメント同士に働く力として計算することはできますが、両方の円盤について積分を計算する必要があり、4次元の積分となり重い計算となりそうです。不可能ではないですが、実際のコンテストでは大きな時間のロスになります。この方法しか思いつかなかった場合は、他の問題を一通り解いた後に残り時間で対応するのがよさそうです。
直前の小問 A2 がヒントになっています。磁石間に働く力を計算する代わりに、円電流間に働く力を計算することができます。磁石間の距離が十分近いことから、円電流同士をグッと近づけた様子を想像すると、局所的には円電流は直線電流とみなせることがわかります。従って、直線電流間に働く力として近似して計算することができます。
球形の磁石間に働く力
小問A4
球形の磁石を吊るしながら沢山つなげていった時に、自重で壊れない範囲でいくつまで繋げられるかを計算します。
まず、最も壊れやすい場所は、一番重量のかかる、一番上の磁石とその直下の磁石とがつながっている箇所です。従って、一番上の磁石が下に繋がった磁石を引きつける引力と、重力とのバランスを考えればよいことになります。
ヒント2にあるように、球形の磁石の作る磁場は大きさのない磁気双極子の作る磁場と同じになります。従って、磁石間にかかる力は磁気双極子間にかかる力として計算することができます。この力は小問 A1 で計算しました。
一番上の磁石が下に繋がった磁石に及ぼす引力は磁気双極子間の力の和として求められます。つながった磁石が十分長いと仮定すると、ヒント1の無限級数の公式により引力を計算できます。この力と重力との釣り合いを調べればいくつまでつなげられるか計算できることになります。計算後に、値が十分大きいこと、すなわち磁石が十分長いことを確認し、仮定が妥当であったことを追認します。
小問5
A4 のように磁石を吊るしながらつなげた状況で、磁石が周囲に作る磁場を計算します。
一般論として、磁石を一列に繋いだ際に発生する磁場を考えると、つなげた箇所から磁場は発生せずに、あたかも両端のみに磁荷があるように振る舞います。このことを念頭に計算を簡略化できないかを考えます。
磁気双極子モーメントは、反対符号を持つ2つの点磁荷の持つ磁荷の値とそれらの間の距離の積として表されます。遠方では、磁荷や距離の個別の値に関係なく、この磁気双極子モーメントの値のみで発生する磁場が決まります。従って、計算上では磁荷と距離を都合のよいように設定してよいことになります。そこで、球形の磁石の作る磁場を計算する際に、距離が球の直径となるような磁気双極子を考えると、接続箇所で正負の磁化を打ち消し合わせることができます。この時に、磁石の持つ磁気双極子モーメントの値は決まっているので、その値を球の直径で割ることで、点磁荷の持つ磁荷の値を計算できます。結果、2つの点磁荷の作る磁場として全体の磁場を計算できることになります。問題の設定から、上方にある点磁荷は十分遠いので、下方にある点磁荷1つの作る磁場として計算すれば十分です。
上記のようなアイディアを思いつかなかった場合でも、直線上に分布する磁気モーメントの作る磁場として全体の磁場を計算することもできます。1次元の積分なので多少の手間はかかるものの比較的容易に計算できるでしょう。
まとめ
この記事では、IPhO2022 スイス大会理論問題1の磁石に関する問題の前半についてテクニカルな面から紹介しました。真正面から扱うと泥沼の積分計算になるので、上手く近似することでなるべく計算量を減らすことが重要になります。
次回は問題の後半について紹介しようと思います。