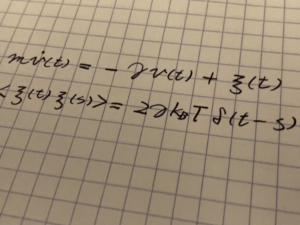国際物理オリンピック2023 理論問題1 コロイド粒子テクニカル編

2023/08/152023/08/20

この記事では、2023年の国際物理オリンピック（International Physics Olympiad = IPhO）日本大会の理論問題1について概観します。計算などの詳細は公式の解答例に記載してあるので、それを繰り返すことはしません。解き方の流れや背景を中心に紹介していきます。

なお、こちらの記事は物理オリンピックの出題範囲程度（≒理系の大学1年生程度）の物理の知識があることを前提にしています。前提知識なく問題の概要を知りたい方は前回の記事をご覧ください。

IPhO2023 理論問題1 コロイド粒子

それでは、IPhO2023 日本大会の理論問題1について背景や解き方を見ていきます。

実際の問題を確認したい方は、IPhO2023のホームページ（英語原文）をご覧ください。以下の紹介では問題のネタバレを含みますので、自力で解きたい方はご注意ください。

全体について

理論問題1は（統計）力学の分野からコロイド粒子についての問題です。水中での微粒子の運動について調べます。

この問題は以下の5つのパートに分かれています。
Part A: コロイド粒子の運動（1.6点）
Part B: 運動の近似（1.8点）
Part C: 電気泳動（2.7点）
Part D: 平均二乗変位（2.4点）
Part E: 水の浄化（1.5点）

細かくパートに分かれていて、点数としても全体的に満遍なく配分されています。前のパートが解けない場合も後のパートが解けることが多いので、途中で詰まっても全体を見渡して取れる箇所を拾っていくことが、実際の試験では重要になるものと思います。

Part A: コロイド粒子の運動

このパートでは、水中での1次元のコロイド粒子の運動を考えています。

問題文中にも与えられていますが、速度 $v(t)$ としたとき、運動方程式は以下です。
$$ M \dot v(t) = -\gamma v(t) + F(t) $$
ここで、$M$ は粒子の質量、$\gamma$ は抵抗係数、$F(t)$ は水分子によるランダムな衝突による力です。この形の方程式は、ランジュバン方程式と呼ばれる確率微分方程式です。アインシュタインのブラウン運動の理論を説明するためにランジュバンによって考案されたものです。現在でも、統計力学の理論的な研究で使われています。

小問A1, A2

通常は、$F(t)$ を正規分布に従う白色ガウスノイズとして計算を進めていくのですが、ここでは、水分子1つ1つによる衝突を具体的に考える力学の問題ととして扱っています。衝突前後の速度の変化は運動量を考えることで力積を使用して記述でき、それ以外の時刻の運動は1階の線形微分方程式
$$ M \dot v(t) = -\gamma v(t)$$
を解くことで求められます。この運動を特徴づける緩和時間は $\tau = M /\gamma$ となります。

Part B: 運動の近似

このパートでは、運動を近似することで平均変位と平均二乗変位の時間発展を求めます。

小問B1

Part A で求めた解から、緩和時間 $\tau$ より離れた異なる時刻では速度の相関が少ないことがわかります。そのことから、時間間隔 $\delta$ で離散化した時に、異なる時刻での速度を独立した確率変数だとみなして近似して計算を進めていきます。すなわち、$n$ 番目の離散時刻での速度を $v_n$ として、
$$
\begin{equation}
\langle v_n \rangle = 0,\quad
\langle v_n v_m \rangle = \left\{
\begin{array}{ll}
C & (n = m) \\
0 & (n \neq m)
\end{array}
\right.
\tag{1}\label{timeCor}
\end{equation}
$$
と仮定します。シンプルな代数計算により、平均変位 $\langle \Delta x(t) \rangle$ が 0 であることがわかります。また、平均二乗変位 $\langle \Delta x(t)^2 \rangle$ も同様に計算できます。

小問B2

前問の結果から平均二乗変位は時間に比例します。これは、拡散での特徴的な挙動です。この時、平均二乗変位が非零の有限値をとるという条件から、同時刻の時間相関の大きさ $C$ は $\delta$ に反比例して増えることになります。このことは、時間相関関数はディラックのデルタ関数（の定数倍）を近似するものであることと対応しています。

Part C: 電気泳動

このパートでは、電荷を持ったコロイド粒子に $x$ 軸方向の電場をかけて、電場に対する応答を考えることで物理量の間の関係式を求めています。

小問C1, C2

電場をかけることでコロイド粒子の密度分布 $n(x)$ には偏りが生じています。偏りが生じると濃度の高いところから低いところへと移動します。誘導に従って微小な領域でのコロイド粒子のミクロなダイナミクスを考えることで、密度の偏りから誘導される粒子の流れを計算できます。この拡散流 $J_D$ は密度の空間微分 $dn/dx$ に比例することがわかります。そして、その比例係数、すなわち、拡散係数 $D$ はミクロな時間相関 $C$ を使用して記述できます。

小問C3

一方で、微小な領域にかかる力の釣り合いを考えます。微小な領域にかかる電場による静電気力は粒子密度 $n$ に比例します。そして、浸透圧による力は $n$ に比例しますが、両側からの力が打ち消し合いネットの力は $dn/dx$ に比例することになります。これらの力の釣り合いから、密度 $n$ とその勾配 $dn/dx$ が比例することがわかります。

小問C4, C5

そして、電場による流れ $J_Q$ は、コロイド粒子の密度 $n$ と終端速度 $u$ の積で近似できます。終端速度は微分方程式の解の極限として、抵抗係数 $\gamma$ を利用して記述できます。平衡状態では拡散流 $J_D$ と打ち消し合うことを利用すると、拡散係数 $D$ と抵抗係数 $\gamma$ の関係式が
$$
D = \frac{kT}{\gamma}
\tag{2}
$$
と求められます。

求められた式は（ブラウン運動についての）アインシュタインの関係式と呼ばれているものです。1905年のアインシュタインの高名なブラウン運動についての論文で導出されました。このパートの設定はその論文に倣ったものになっています。（導出に至るまでの道筋は多少異なります。）

Part D: 平均二乗変位

このパートでは、平均二乗変位の振る舞いについて調べます。

小問D1

ここでは、実験的に得られた変位のヒストグラムが与えられ、アボガドロ数を推定します。

ヒストグラムから、実験における $\langle \Delta x(t)^2 \rangle$ の値を計算できます。一方で、Part C の計算から$\langle \Delta x(t)^2 \rangle = 2Dt$ なので、拡散係数がわかります。あとは、アインシュタインの関係式 (2) を用いることで、ボルツマン定数が求められ、アボガドロ数も計算できることとなります。

小問D2

ここでは、Part C のように電場がかかっている場合の平均二乗変位の振る舞いを調べます。

問題の誘導のように、終端速度 $u$ を使用して、速度を $v(t) = u + v_n$ と近似します。ここで、$v_n$ は式 (1) を満たす確率変数です。クロスタームが平均を取ると消えることに注意すると、
$$ \langle \Delta x(t)^2 \rangle = u^2t^2 + 2Dt $$
と計算できます。時間の小さい時は第2項が、時間の大きい時は第1項が支配的となります。すなわち、短い時間では水分子の衝突による撃力の影響が支配的となり、長い時間ではランダムな運動よりも一定速度の移動の影響が支配的となります。

小問D3

ここでは、能動的に移動する微生物の運動について調べます。

微生物は時間間隔 $\delta_0$ ごとにランダムに $\pm u_0$ の速度で泳動します。ランダム変数 $u_k\ (k = [t / \delta_0])$ を導入することで、速度は $v(t) = u_k + v_n$ と書けます。$u_k$ はランダムに $\pm u_0$ の値を取るので、
$$
\langle u_k \rangle = 0,\quad
\langle u_k u_l \rangle = \left\{
\begin{array}{ll}
u_0^2 & (k = l) \\
0 & (k \neq l)
\end{array}
\right.
$$
を満たします。また、微生物の速度と水分子による揺動に相関はないので、$\langle u_k v_n \rangle = 0$ となります。これらの関係式を用いると、前問と同様に平均二乗変位を計算できます。

泳動の持続時間 $\delta_0$ よりも短い範囲では、前問と同様の振る舞いをします。一方、それよりも長い時間では泳動がランダムなために再び拡散的な振る舞いをすることがわかります。

Part E: 水の浄化

このパートでは、土の微粒子の凝集して水を浄化することを考えます。

水中では粒子の表面は電離したり周囲の荷電粒子を吸着することで帯電しています。そのため、粒子同士は静電気力で反発しています。この静電気力は粒子同士に働くファンデルワールス力による引力より優勢です。

水に電解質を加えていくと、粒子の周囲に粒子の持つ電荷と反対符号のイオンが集まり、電気二重層を形成します。それにより、粒子の持つ電荷が遮蔽されて静電気的な斥力が弱まっていくこととなります。電解質の濃度が閾値を超えると、ファンデルワールス力の方が優勢となり粒子が凝集することとなります。

なお、このパートのは以前のパートまでとは独立して解けるようになっています。

小問E1

2粒子間のポテンシャルは、粒子間距離を $d$ として、
$$
U(d) = – \frac{A}{d} + B’ e^{-d/\lambda}
\tag{3}
$$
という形で与えられます。ここで、$A, B’$ は正の定数で、 $\lambda$ は電気二重層の厚さを表し、電解質の濃度を $c$ とすると、 $\lambda \propto c^{-1/2}$ となります。第1項と第2項はそれぞれファンデルワールス力と静電気力に起因します。なお、このポテンシャルは、リャーギン・ランダウ・フェルウェー・オーバービーク理論により求められるものです。

十分大きな粒子を考えると、水中の粒子はすぐに終端速度に達することになります。従って、粒子は常にポテンシャルの傾きを降りるように移動することがわかります。通常の（散逸のない）力学のように慣性によってポテンシャルを登ることはありません。

濃度 $c$ の低い場合は電気二重層の厚み $\lambda$ が大きくなります。$\lambda$ が $A$ よりも十分大きな場合での挙動を考えましょう。粒子間距離 $d$ が $\lambda$ 程度の場合、式 (3) の第1項はほぼ消えて、ポテンシャルは正の値を持つことがわかります。一方で、$d$ が $\lambda$ よりも十分大きなところでは、式 (3) の第1項の方が優勢になりポテンシャルが負になることがわかります。従って、$d$ が $\lambda$ よりも大きなどこかでポテンシャルが極小点を持つこととなります。

$\lambda$ が小さくなると、式 (3) は第1項のみ残り、ポテンシャルは谷を持ちません。従って、電解質の濃度 $c$ を増やしていくとどこかの時点でポテンシャルの谷が消えることがわかります。谷が消える際には、変曲点での微分が0になるので、
$$U'(d) = 0,\quad U^{\prime\prime}(d)=0$$
を解くことで、閾値となる $c$ を求められます。