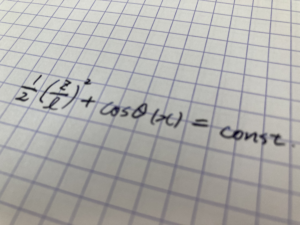この記事では、2023年の国際物理オリンピック(International Physics Olympiad = IPhO)日本大会の理論問題3について紹介します。計算などの詳細は公式の解答例に記載してあるので、それを繰り返すことはしません。解き方や背景を中心に紹介します。
なお、こちらの記事は物理オリンピックの出題範囲程度(≒理系の大学1年生程度)の物理の知識があることを前提にしています。前提知識なく問題の概要を知りたい方は前回の記事をご覧ください。

IPhO2023 理論問題3 水の表面張力
それでは、IPhO2023 日本大会の理論問題3について紹介します。
実際の問題を確認したい方は、IPhO2023のホームページ(英語原文)をご覧ください。以下の紹介では問題のネタバレを含みますので、自力で解きたい方はご注意ください。
全体について
理論問題3は水の表面張力についての出題です。力学的な考察から水の表面がとる形状について議論します。
問題は以下の3つのパートに分かれています。
Part A: 水滴の合体
Part B: 鉛直な板との相互作用
Part C: 2つの棒との相互作用
問題の内容として、Part A はそれ以降のパートと独立しています。Part B, C は密に関連しているのでしっかりと前の小問から点数を取っていく必要があります。
以下では、それぞれのパートについて見ていきます。
表面張力について
水分子同士は引力相互作用をするために、隣接する水分子のポテンシャル・エネルギーは負になっています。水の表面に存在する水分子を考えると、隣接する水分子の数がバルク中よりも減るために、それに対応する負のポテンシャル・エネルギーが無くなります。従って、水の表面では、水のバルク中よりも(自由)エネルギーが高くなります。その単位面積あたりのエネルギーの差は物質固有の値を持ち、$\gamma$ として与えられます。
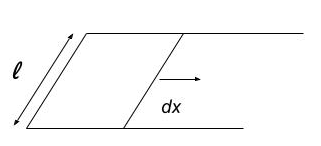
下図に示すマクスウェルの枠について考えましょう。枠の左側には水の膜が張ってあります。今、枠の右端を $dx$ だけ拡げる状況を考えましょう。その時、水面が上下両面あることを考えると、表面のエネルギーは $2\gamma l dx$ 増加します。従って、枠の右端には引きつけるように $2\gamma l$ の力が働いていることがわかります。これは、水面の単位長さあたりに働く力が $\gamma$ であることを意味します。そのため、$\gamma$ は表面張力と呼ばれます。このように、表面の単位面積あたりのエネルギーの大きさと、表面の単位長さあたりに働く力は等しくなります。
Part A: 水滴の合体
ここでは、疎水性の板の上で水滴が合体する状況を考えます。
疎水性の板の上では(重力が無視できる範囲で)表面積が最も小さくなる球形を取ります。同じ大きさの球状の水滴が合体して大きな水滴を作る状況を考えます。
小問 A1
水滴が合体した際に、合体後の水滴が跳ね上がる高さを求めます。水滴は合体により表面積が小さくなるのでその分だけエネルギーが低くなります。そのエネルギー差のうち一部が運動エネルギーに変換されて水滴が跳ね上がります。運動エネルギーに変換される割合が問題文中に仮定されているので、合体後の運動エネルギーが計算でき、跳ね上がる高さも求められます。
Part B: 垂直な板との相互作用
このパートでは、水に垂直に板を挿入した状況での水面の形状について考えます。
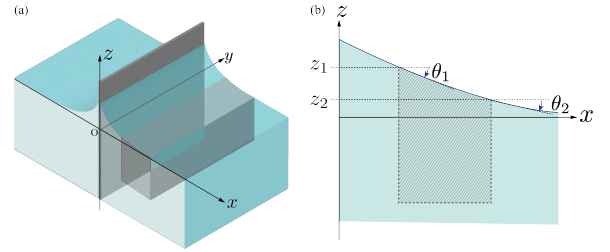
水に親水性の板を挿入した際には、水と板の接触を増やした方がエネルギー的に有利なので、板を中心に山状に水面が分布します。一方で、疎水性の板を挿入した際には、接触を減らす方が有利なので、谷状に水面が分布します。下図を参照してください。
小問 B1
水圧による圧力の変化を求める基本問題です。
小問 B2
前掲の図の右側で斜線で示された部分に働くネットの圧力を求める問題です。問題文中にもヒントがあるように大気圧は全体として釣り合うので、水圧による圧力変化のみ考慮すればよいです。斜線部の左側から働く圧力と右側から働く圧力とを積分して差を取ります。
小問 B3
前問の圧力による力を表面張力で表す問題です。水平方向の力の釣り合いを考えることで単純に導出できます。
小問 B4
水の表面での保存量を求める問題です。前問の結果を見ると、斜線部の左側に関する物理量のみ含む項と、右側に関する物理量のみ含む項とにきれいに別れていることがわかります。移項して整理することで、左側に関する物理量が右側に関する物理量と等しいという等式を作れ、その物理量の表式は左右で同じなので、その量が保存量となることがわかります。
小問 B5
前問で求めた保存量から微分方程式を求める問題です。丁寧な誘導に従って代数的な式変形を行うと、2階の線形微分方程式が得られます。それを解くと、指数的に増減する解が得られます。遠方で水面の高さが0となるという境界条件を用いることで、指数的に減少する解が得られます。
Part C: 2つの棒との相互作用
このパートでは水面に2つの棒を平行に並べた際の相互作用について考えます。
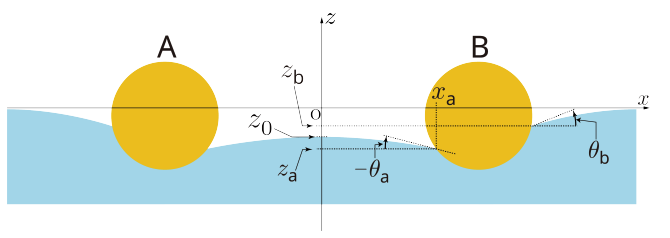
小問 C1
棒に働く力を求めます。小問 B2 で計算したように水圧による力を計算し、小問 B3 で計算したように表面張力による力を計算して、それらの合計としてネットの力を求められます。
小問 C2
前問で求めた力を式変形します。小問 B4 で導出した保存量を使うと、棒の内側に働く力は2つの棒の中点での物理量で、棒の外側に働く力は無限遠での物理量で表すことができます。結果、とてもシンプルな式に変形できます。得られた表式から棒同士には引力が働くことがわかります。保存量を使用して式を簡略化するのはよく使用されるテクニックです。
小問 C3
2つの棒の中点での水面の高さを求める問題です。小問 B5 の結果から、水面の形状は指数関数で表されることがわかります。そのことを用いると棒の間での水面の形状の式を求めることができます。その結果、棒と内側で接する水面の座標を用いることで、中点での水面の高さを求められます。
まとめ
この記事では、IPhO2023 理論問題3の水の表面張力に関する問題を紹介しました。力学的な考察から導出した微分方程式を解くことで水の表面の形状を求めるという流れでした。物理的な考察の分量が比較的少なく、代数的な計算の割合が多い印象でした。また、Part A とそれ以降は完全に独立に解けますが、Part C では Part B での考察を利用する箇所も多かったです。途中でつまづくと点数を取りにくく、差がつきやすい問題だったのではないかと思います。