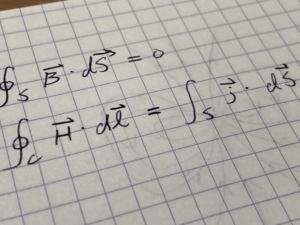この記事では、2022年の国際物理オリンピック(International Physics Olympiad = IPhO)スイス大会の理論問題1の後半部分について解き方に踏み込んで紹介していきたいと思います。計算などの詳細は公式の解答例に記載してあるので、それを繰り返すことはしません。どういった考え方をすると解き方を思いつくのかというところに主眼を置きたいと思います。
前半部分については前回の記事で紹介しています。
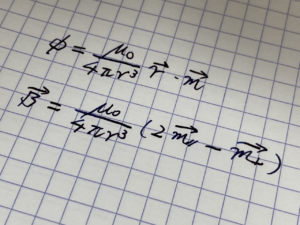
なお、こちらの記事は物理オリンピックの出題範囲程度(≒理系の大学1年生程度)の物理の知識があることを前提にしています。前提知識なく問題の概要を知りたい方はこちらの記事をご覧ください。

IPhO2022 理論問題1 磁石
それでは、IPhO2022 スイス大会の理論問題1の後半(Part B から)について考え方を見ていきます。
実際の問題や解答例を確認したい方は、物理チャレンジのホームページ(日本語訳)か IPhO2022 のホームページ(英語原文)をご覧ください。以下の紹介では問題のネタバレを含みますので、自力で解きたい方はご注意ください。
Part B: 強磁性体との相互作用
このパートでは、磁石と強磁性体との間の相互作用について考えます。
パートを通しての考え方1:鏡像法
ヒント5にもあるように、透磁率が大きい物体に対しては、磁力線が表面に対してほぼ垂直になります。このことは、強磁性体の表面での磁気ポテンシャルがほぼ一定となることを意味します。そのような磁場を作るように強磁性体の表面に磁化が誘起されるわけですが、その磁化密度を計算することは一般的に手間がかかります。その代わりに、ヒント4にあるように境界の外側に仮想の磁場源を置くことで境界より手前での磁場を計算できる場合があります。
まず、簡単な場合として平面状の強磁性体の近くに点磁荷を置くことを考えます。この時に、境界の平面では磁気ポテンシャルが一定にならなければいけません。元の点磁荷に対して平面から鏡像の位置に符号が反対の磁荷を置くことを考えましょう。そのような仮想磁荷を置くと平面上では磁気ポテンシャルが0となり、一定となることがわかります。このように、鏡像の位置に符号が反対の磁荷を置くことで境界条件を満たす磁場を作ることができ、境界より手前の磁場は元の磁荷と仮想磁荷とが作る磁場として計算することができます。
次に、磁気双極子を平面状の強磁性体の近くに磁気双極子を置くことを考えます。磁気双極子の作る磁場は符号が反対の磁荷を無限小の距離だけ離して並べた際に作られる磁場と一致します(この時、磁荷の値と距離の積が、磁気双極子モーメントの値と一致するようにします。)。強磁性体の近くに磁気双極子を置いたときの磁場を再現するためには、これら2つの磁荷の鏡像の位置に符号が反対の磁荷を置けばよいことになります。このことは、磁気双極子の鏡像の位置に、(ベクトル量として)鏡像対称で反対向きの磁気双極子モーメントを持つ磁気双極子を置くことと等価です。
パートを通しての考え方2:場の連続性
物体の境界での場の連続性について考えます。
物体の境界に微小な円を描き、その円を境界の法線方向に上下に無限小だけ押し出した円柱状の領域を考えましょう。その領域について Gauss の定理を適用すると磁束密度の法線成分が境界の内外で同じであることがわかります。
一方、物体の境界に微小な線を描き、その線を境界の法線方向に上下に無限小だけ押し出したループ状の領域を考えます。物体表面に電流が流れていない時、その領域について Ampere の定理を適用すると磁場の接線成分が境界の内外で同じであることがわかります。
このように、物体の境界では磁束密度の法線成分と磁場の接線成分が連続となります。
小問B1
強磁性体の近くに球形の磁石を置いた際の磁力線を描くという内容の問題です。
強磁性体の表面より手前側については、元の磁石と表面について鏡像の位置に反対を向くように仮想的に磁石を置けば磁場を再現することができます。
強磁性体の内部については、場の連続性を考慮して磁力線を接続していきます。空間から強磁性体に入る際に、磁束密度の法線成分が一定で、接線成分が比透磁率倍になります。そのため、ほぼ垂直に入った磁束密度が表面で大きく屈折して入っていくことがわかります。
以上の考察をもとに磁力線を描くことで正しい磁力線を結ぶことができます。
小問B2
球形の磁石を強磁性体の板に接触させた際に、安定な平衡状態を求めるという問題です。
磁石の磁化と板の法線とのなす角が $\theta$ の時の相互作用のエネルギーを考えます。磁石の鏡像を考えると、$-\theta$ の方向を向く仮想磁石を置いたとみなすことができます。片方の磁気双極子がもう片方の磁気双極子の場所に作る磁場は計算できるので、相互作用のエネルギーを計算することができます。相互作用のエネルギーが極小になる箇所を求めると、磁化と板の法線は平行または反平行($\theta = 0, \pi$)であることがわかります。
なお、公式の解答では元の磁気双極子と鏡像の磁気双極子が作る磁場が平行な時に安定になるとして解答していますが、安定性の解析としては不十分であるように思われます。実際、磁石の磁化と板の法線が垂直になる場合にも、磁気双極子と鏡像の磁気双極子が作る磁場が平行になるという条件を満たすので、この場合を論理的に除くことができません。磁石を回転させると鏡像の磁石も回転するために、単純に磁気双極子と磁場が平行であるかと確認するだけでは不十分です。
小問B3
この問題では、コイン形の磁石を2つの円筒形の強磁性体で挟んだ時に、強磁性体にかかる力を計算します。
強磁性体にかかる力を直接積分で求めるのは積分の次元が高くかなりしんどそうです。そのため、力を直接計算するのではなく、エネルギーを計算をして強磁性体間の距離で微分することで力を求めるという方針を立てます。エネルギーを求める際に、磁石の厚みも変化させると、磁石の持つエネルギーも変化するので考慮する事項が多くなります。そのため、小問A2のように磁石を円電流で置き換えることを考えます。すなわち、円電流を挟む強磁性体を引き離すのにかかる力を計算する問題を解くこととします。
まず、強磁性体の表面で磁場が垂直になることと、強磁性体の隙間が十分に小さいことから、隙間の磁場は円筒の軸に平行になります。隙間の微小領域に Ampere の定理を適用すると、磁場は円電流の内側と外側とでそれぞれ一定になることがわかります。隙間のうちで電流を囲む微小領域にAmpere の定理を適用すると内側と外側の磁場についての関係式が1つ得られます。
また、ヒントより強磁性体のサンドイッチの外側に漏れ出る磁場は無視できます。そのため、片方の強磁性体についてGauss の定理を考えると、強磁性体の隙間で、円電流の内側から入ってきた磁束は、円電流の外側に出ていくことがわかります。これから、内側と外側の磁場について2つ目の関係式が得られます。
これらの2つの関係式を用いることで、円電流の内側と外側の磁場の大きさを求めることができます。磁場の大きさがわかると隙間の空間の持つ磁場のエネルギーが計算できます。このエネルギーを隙間の大きさで微分することで強磁性体に働く力を求めることができます。
Part C: (反)強磁性秩序
このパートでは、球形の磁石を2次元格子上に並べた際に、安定な配置での磁化の向きを求めます。
パートを通しての考え方
安定性を求める際には、回転と変位について安定であることを確かめます。回転についての安定性は、ある磁石の磁化と周りの磁石が作る磁場が平行であることを確かめればよいです。変位についての安定性は、隣り合う磁石と引き合っていることを確かめれば十分です。
小問C1
正方格子上に並べた際の安定配置を求め、安定性を示します。
問題のリード文から磁化が互いに平行な方向を向いている(強磁性秩序)のか、反平行な方向を向いている(反強磁性秩序)のかどちらかであろうと当たりをつけます。直感的にも明らかですが、平行だと仮定すると磁化に垂直な方向に隣り合う磁石同士が反発してしまい、変位について安定になりません。一方、反平行な場合はこの変位について安定になります。後は、4隣接の磁石が作る磁場が磁化と平行であること、すなわち回転について安定であることを示せば十分です。
小問C2
三角格子上に並べた際の安定配置を求め、安定性を示します。
磁化が平行な方向を向いている(強磁性秩序)の際に安定すると当たりをつけられます。磁化に対して、60度方向と120度方向の磁石と引き合うかを考えます。それらの磁石が作る磁場の磁化に垂直な成分と平行な成分に分けてそれぞれ計算できるので、磁場中の磁化のエネルギーとして相互作用のエネルギーを計算できます。結果、磁石間に引力が働くことが確かめられます。後は、回転についての安定性として6隣接の磁石が作る磁場と磁化が平行であることを示せば十分です。
まとめ
この記事では、IPhO2022 スイス大会理論問題1の磁石に関する問題の後半についてテクニカルな面から紹介しました。Part B では、鏡像法や場の連続性など、電磁気学の概念を使いこなす必要があり、難易度の高い問題が続きました。Part C は、Part B と比較すると、磁場の方向やエネルギーを計算するシンプルな問題となっています。実際の大会では、Part B で燃え尽きずに Part C を着実に拾っていくことが点数を分けたのではないかと想像します。